如下图，在平面坐标系下，物体 (质点)沿曲线CABD运动，考虑如何描述从点A到点B的运动属性。

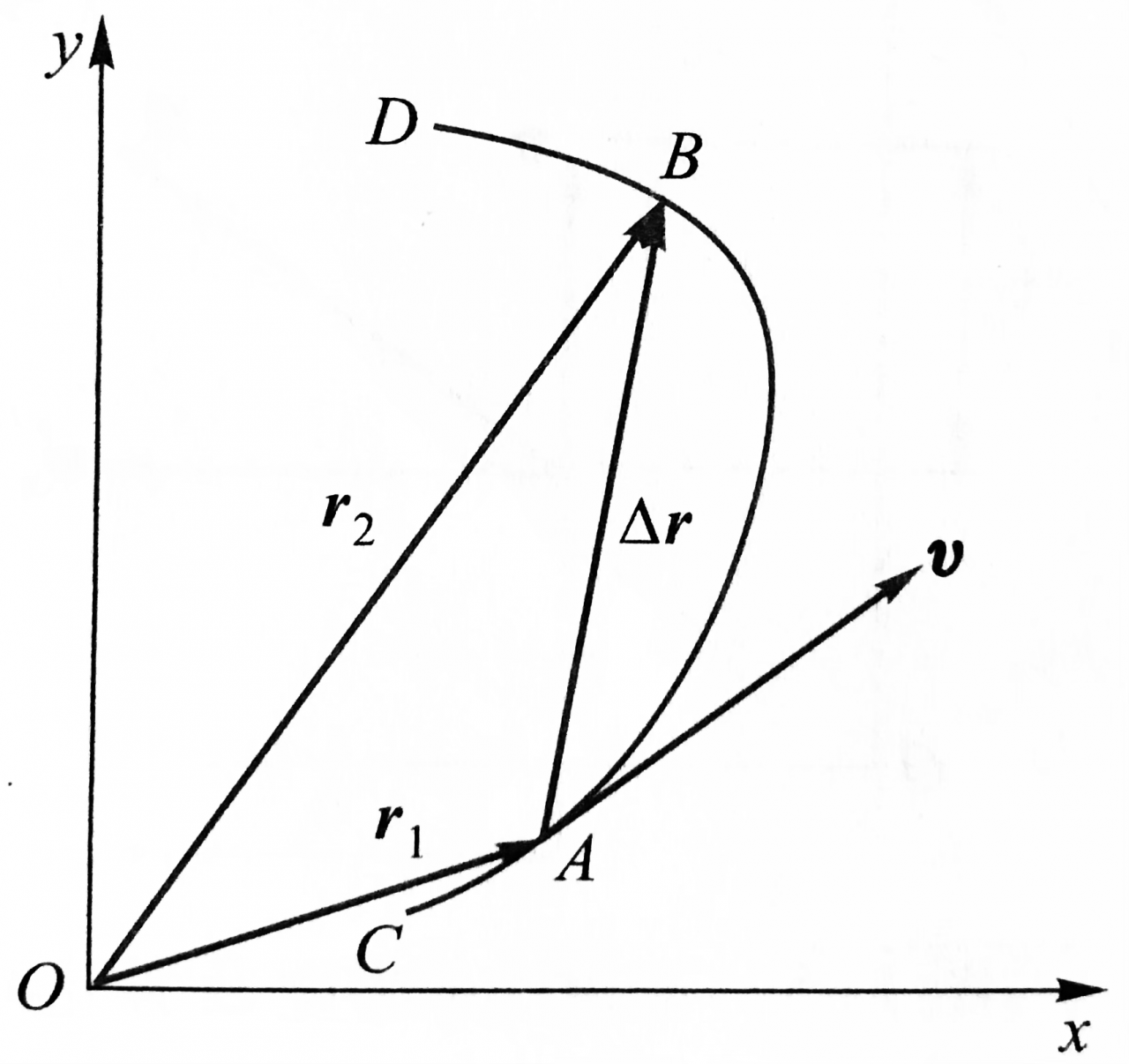
首先考虑到的，是物体的位置发生了什么样的变化？物体空间位置的变化，是由位移这个物理量来描述的，对应于图中的矢量 Δr 。

其次，物体从A点运动到B点，是在一段时间内发生的。换句话说，如何度量物体运动的是快还是慢？一段位移发生的快慢，是由速度这个物理量来描述的。

所以，位移和速度是描述运动属性的两个关键物理量。

速度的定义

物体从A点运动到B点，其平均速度定义为：

这个速度称为 从A到B的平均速度。

平均速度是一个矢量，其方向是和位移的方向保持一致的。

速度直接反映的物理意义，是物体运动的剧烈程度；如果从物体运动的位移-时间图像的角度分析，平均速度是位移-时间图像上A和B两点之间割线的斜率。

因为位移可以分解为沿着x轴和y轴的矢量分量：

所以速度也可以表示为：

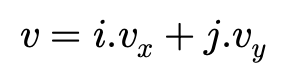
即速度可以分解为沿x轴和y轴方向的速度分量。

在某一时刻的瞬时速度该如何理解呢？

首先要明确，瞬时速度就是平均速度在 Δt 趋近于0时的极限值，即：

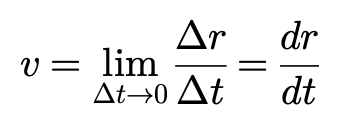
某一时刻 t0 的运动速度，等于位移函数对时间求导的导函数在 t0 时的值。从位移-时间函数图像上说，也就是函数图像 在 t = t0 处的切线斜率。

同样的，瞬时速度也可以分解为 坐标轴方向的分矢量和：

上述为二维空间下速度的定义。将之直接推广到三维空间，增加一个z轴维度即为三维空间中关于速度的定义。